728x90
선택 정렬(Selection Sort)
선택 정렬(Selection Sort)은 정렬 알고리즘 중에서 개념적으로 가장 간단한 방식 중 하나로, 배열에서 가장 작은(또는 큰) 값을 반복적으로 찾아서 순서대로 앞쪽으로 옮기는 방식입니다. 구현이 매우 직관적이고 코드량도 적기 때문에 알고리즘 입문자에게 자주 소개되는 알고리즘입니다. 하지만 시간 복잡도가 O(n²)으로, 데이터 양이 많아질수록 성능이 크게 떨어져 실무에서는 거의 사용되지 않습니다.
1. 선택 정렬이란?
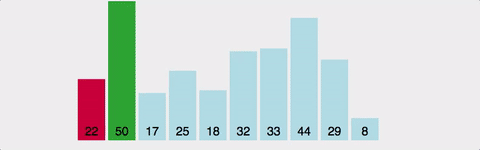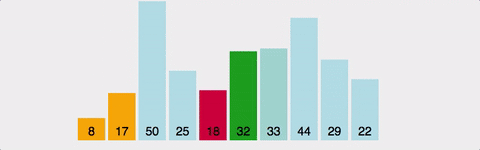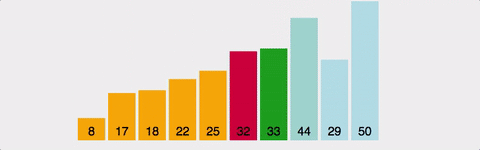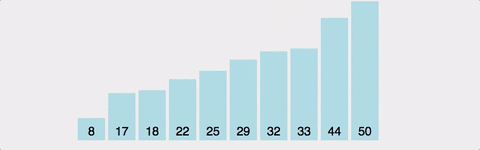
선택 정렬은 매 반복마다 가장 작은(또는 큰) 원소를 찾아서 현재 위치에 있는 원소와 교환하는 방식입니다.
동작 방식 (오름차순 기준)
- 리스트의 첫 번째부터 시작하여 가장 작은 값을 찾음
- 현재 위치의 값과 가장 작은 값을 교환
- 두 번째 위치부터 반복...
- 모든 요소를 정렬할 때까지 반복
장점
- 구현이 매우 간단하고 직관적
- 메모리 추가 공간 필요 없음 (in-place)
- 교환 횟수가 상대적으로 적음 (최대 n-1번)
단점
- 시간 복잡도가 O(n²)로 느림
- 실제 프로젝트에서는 거의 사용되지 않음
- 안정 정렬이 아님
2. 예시
초기 배열 : [64, 25, 12, 22, 11]
- 첫 번째 패스 : 가장 작은 11을 첫 위치와 교환 → [11, 25, 12, 22, 64]
- 두 번째 패스 : 12를 두 번째 위치와 교환 → [11, 12, 25, 22, 64]
- 세 번째 패스 : 22를 세 번째 위치와 교환 → [11, 12, 22, 25, 64]
- 네 번째 패스 : 이미 정렬됨
최종 결과 : [11, 12, 22, 25, 64]
3. 언어별 구현 예시
a. Python
def selection_sort(arr):
n = len(arr)
for i in range(n):
min_idx = i
for j in range(i+1, n):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]b. C++
void selectionSort(vector<int>& arr) {
int n = arr.size();
for (int i = 0; i < n - 1; ++i) {
int min_idx = i;
for (int j = i + 1; j < n; ++j)
if (arr[j] < arr[min_idx])
min_idx = j;
swap(arr[i], arr[min_idx]);
}
}c. Java
void selectionSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
int min_idx = i;
for (int j = i + 1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
int temp = arr[min_idx];
arr[min_idx] = arr[i];
arr[i] = temp;
}
}d. JavaScript
function selectionSort(arr) {
const n = arr.length;
for (let i = 0; i < n - 1; i++) {
let minIdx = i;
for (let j = i + 1; j < n; j++) {
if (arr[j] < arr[minIdx]) minIdx = j;
}
[arr[i], arr[minIdx]] = [arr[minIdx], arr[i]];
}
}
4. 시간 복잡도 분석
| 케이스 | 시간 복잡도 |
| 최악의 경우 | O(n²) |
| 평균 | O(n²) |
| 최선 | O(n²) |
| 공간 복잡도 | O(1) |
| 정렬 안정성 | 불안정 정렬 |
- 항상 전체를 탐색해야 하므로 최선도 O(n²)
- 제자리 정렬이지만 안정 정렬이 아님 (같은 값을 교환할 수 있음)
5. 마무리
- 선택 정렬은 리스트에서 가장 작은 값을 골라 자리를 바꾸는 단순한 방식의 정렬 알고리즘입니다.
- 시간 복잡도는 O(n²)로 비효율적이지만, 개념이 직관적이고 구현이 쉬워 학습용으로 적합합니다.
- 안정 정렬이 아니며, 실제 대규모 데이터에는 부적합하므로 상황에 따라 더 나은 알고리즘을 선택하는 것이 중요합니다.
함께 보면 좋은 자료
외부 사이트 :
블로그 글 :
[정렬] 꼭 알아야 할 7가지 정렬 알고리즘 비교 정리
정렬(Sorting) 정렬(Sorting)은 데이터를 일정한 순서(오름차순, 내림차순 등)로 재배치하는 알고리즘입니다. 정렬은 탐색, 최적화, 통계 처리 등 거의 모든 컴퓨터 과학 문제의 전처리 단계로 중요하
dachaes-devlogs.tistory.com
728x90
'코딩테스트 > 알고리즘' 카테고리의 다른 글
| [퀵 정렬] 피벗으로 나누고 빠르게 정복하는 정렬 알고리즘 (0) | 2025.05.02 |
|---|---|
| [삽입 정렬] 카드를 정렬하듯, 데이터를 끼워 넣는 알고리즘 (0) | 2025.05.02 |
| [버블 정렬] 하나씩 비교하며 정렬하는 알고리즘 (0) | 2025.05.02 |
| [정렬] 꼭 알아야 할 8가지 정렬 알고리즘 비교 정리 (0) | 2025.05.02 |
| [Queue] 줄 서서 처리하는 선입선출(FIFO) 자료구조 (0) | 2025.04.29 |